본 글은 알고리즘 설계 과목에서 작성한 코드를 기반으로 한 글입니다.
💡 Exchange sort
정렬되지 않은 배열에서, Index 키와 나머지 키를 비교하여, 가장 작은 키를 인덱스 순차적으로 위치시키는 알고리즘
void exchangeSort(vector<int>&arr) {
int N = arr.size();
for(int i = 0; i < N - 1; i++) {
for (int j = i + 1; < N - 1) {
if (arr[j] < arr[i]) {
swap(arr[i], arr[j])
}
}
}
}
시간복잡도는 항상 모든 배열의 내용을 비교하므로 O(n^2)이며 배열 내 정렬이 일어나므로 공간 복잡도는 O(1)이다.
💡 Insertion sort
정렬되지 않은 배열에서 순차적으로 키를 선택해 오름차순으로 정렬 중인 배열의 앞부분에 삽입하는 알고리즘
void insertSort(vector<int>&arr) {
int N = arr.size();
for(int i = 1; i < N; i++) {
key = arr[i];
j = i - 1;
while(j > 0 && arr[j] > key) {
swap(arr[j+1], arr[j])
j--
}
arr[j+1] = key;
}
}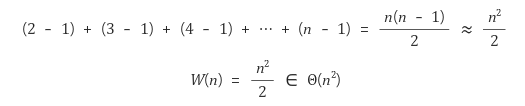
배열의 첫번째 인덱스를 제외한 마지막 인덱스까지 검사하므로 n-1개가 i값이 된다. 배열 내 제자리 정렬이 일어나므로 공간 복잡도는 O(1)이다.
💡 Selection sort
키와 인덱스를 저장하는 변수를 이용해 가장 작은 키의 인덱스를 저장해뒀다가 반복이 끝나면 교환하는 방식의 알고리즘이다. 즉, 교환정렬의 오버헤드를 줄인 방법이다.
void selectionSort(vector<int>&arr) {
int N = arr.size();
for(int i = 0; i < N - 1; i++) {
min = i;
for (j = i + 1; j < N; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
swap(arr[min], arr[i]);
}
}
i-1번 비교가 일어나며 배열 내 제자리 정렬이 일어나므로 공간 복잡도는 O(1)이다.
💡 Merge sort
하나의 리스트를 두 개의 크기로 분할하고 분할된 부분을 정렬한 후 두 개의 정렬된 리스트를 합해 전체가 정렬된 리스트가 되도록 하는 방법이다. 때문에 추가적인 리스트가 필요해 공간 복잡도는 O(N)이 된다.
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l + (r - 1) / 2;
mergeSort(arr, l, m);
mergeSort(arr, m + 1, r);
merge(arr, l, m, r);
}
}💡 Quick sort
1. 리스트 안의 한 요소 (Pivot)을 선택한다.
2. Pivot을 기준으로 Pivot보다 작은 요소는 왼쪽으로, 큰 요소는 오른쪽으로 옮긴다.
3. Pivot을 제외한 리스트를 재정렬한다.
4. 분할된 부분 리스트들에 대해 정렬을 반복한다.
5. 분할된 부분 리스트에서도 Pivot을 정하고 이러한 과정을 반복한다.
void quickSort(int arr[], int l, int r) {
if (l < r) {
int p = partition(arr, l, r);
quickSort(arr, l, p - 1);
quickSort(arr, p + 1, r);
}
}
int partition (int arr[], int l, int r) {
int pivot = arr[r];
int i = l - 1;
for (int j = l; j <= r - 1; j++) {
if (arr[j] <= pivot) {
i++;
swap(arr[i], arr[j]);
}
swap(arr[i + 1], arr[r]);
return i + 1;
}
}
💡 Shell sort
1. 첫번째 gap으로 arr / 2를 설정한다. 각 gap은 홀수여야 하므로 짝수일 경우 +1을 통해 홀수로 만들어준다.
2. 0번째부터 gap이전의 요소까지 gap만큼 떨어져 있는 비연속적인 배열로 나눈다.
3. 각 비연속적인 배열을 gap만큼 떨어진 원소들을 통해 삽입정렬로 정렬한다.
4. gap을 1/2 해주어 gap이 0보다 클때까지 이과정을 반복한다.
void shellSort(int arr[], int n) {
int gap, i, j, key;
for (gap = n / 2; gap > 0; gap / 2) {
if (gap % 2 == 0) {
++gap;
}
for (i = gap; i <= n; ++i) {
key = arr[i];
for (j = i; j >= gap && arr[j - gap] > key; j+=gap) {
arr[j] = arr[j - gap];
}
arr[j] = key;
}
}
}'Language > C++' 카테고리의 다른 글
| Let's measure time complexity by n^3 and 2^n (0) | 2023.03.06 |
|---|---|
| [C++ / 백준 11050] 이항 계수 1 (0) | 2021.08.23 |
| [C++ / 백준 1934] 최소공배수 (0) | 2021.08.20 |
| [C++ / 백준 2609] 최대공약수와 최소공배수 (0) | 2021.08.19 |
| [C++ / 백준 1037] 약수 (0) | 2021.08.18 |